Нормативні документи відносно ЗНО - 2021-2022 року. (Український центр оцінювання якості освіти)
Шановні учні, пропоную вам матеріали, які допоможуть краще зрозуміти навчальний матеріал.
Підручник Математика 10 клас О. Істер.
Підручник Математика 11 клас О. Істер
Алгебра і початки аналізу.
Тема уроку: Функція.
Повідомлення про
функцію
Поняття функції ввели:
П. Ферма (1601-1665)
Р. Декарт(1596-1650)
І. Ньютон (1643-1727)
Г.В. Лейбніц (1646-1716)
Слово «функція» (з латинської - виконання) німецький математик Лейбніц вживав в 1673
році. В 1698 Лейбніц ввів терміни «змінна
і «константа». Визначення функції, «Функцією змінної величини називають
кількість, утворена яким завгодно способом з цієї змінної», належить
швейцарському математику Бернуллі.
Л. Ейлер ввів означення: «Функція змінної кількості є аналітичний
вираз, складений будь –яким чином з цієї кількості і чисел»
М. І. Лобачевський ввів поняття незалежної змінної, або
аргументу, а змінну у – залежною
змінною, або функцією.
Німецький вчений Л. Діріхле ввів способи задання функції:
аналітичний, табличний, графічний.
Табличний спосіб використовується при введенні інформації в
ЕОМ,
Графічним способом введення функції користуються при дослідженнях з використанням самописних приладів: барограф для запису атмосферного тиску, осцилограф – для запису змін електричного струму. термограф – для запису змін температури. Це криві – барограма, осцилограма, електрокардіограма,термограма. Показникова функція фіксує кількість радіактивних ізотопів для діагностики при захворюваннях нирок, степенева функція характеризує процес використання авіаліній. Поняття функції використовується при описанні взаємодії елементів електричного кола в фізиці.
Презентація Функція
Відеоуроки
Практичне заняття. Побудова графіків функцій
https://www.desmos.com/calculator/nnca8itinb?lang=uk
Тема. Графіки основних видів функцій
Графіком функції у = f(х) називають множину всіх точок (х; у) координатної площини, у яких абсциси належать області визначення функції, а ординати обчислюють за формулою у = f(х).
З попередніх класів ми вже знаємо вигляд графіків функцій
![]()
Функція у = kх + І
Функцію вигляду у = kх + І, де k і І — деякі числа, називають лінійною.
Графіком функції у = kх + І є пряма  мал.1
мал.1
 мал. 3
мал. 3
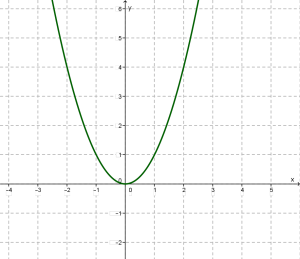
Функція у = х2
Графіком функції у = х2 є парабола, гілки якої напрямлені вгору, а вершиною є точка (0; 0) (мал.2).
Функція у = ![]()
Графіком функції у = ![]() є гілка параболи, що лежить у І чверті координатної площини (мал.5).
є гілка параболи, що лежить у І чверті координатної площини (мал.5).

Мал. 4
 мал.5
мал.5
Функція у =k/x,k ≠ 0
Графіком функції у = k/x, k ≠ 0 є гіпербола, гілки якої лежать у І і III чвертях, якщо k > 0 (мал. і у II і IV чвертях, якщо k < 0 (мал. ).


мал 6,7
Функція у = ах2 + bх + с, а ≠ 0
Графіком функції у = ах2 + bх + с, де а ≠ 0, є парабола з вершиною в точці А(хв; ув) (мал. 4.8). її можна побудувати в такий спосіб:
1) знайти ще кілька точок, що належать параболі (під час побудови можна використати симетрію параболи відносно прямої х = хв);
2) сполучити отримані точки плавною лінією.
Приклад 1. Схематично побудувати графік функції та знайти її проміжки зростання і спадання:
1) у = -3 + 2;
2) у = х2 - 2х + 4.

Розв’язання. 1) На малюнку зображено графік функції у = -3х + 2. Це пряма, яку проведемо через точки (0; 2) і (1; -1). Функція спадає на проміжку (-∞; +∞).


Мал.6
2) Графіком функції у = х2 - 2х + 4 є парабола, гілки якої напрямлені вгору. Знайдемо координати вершини параболи: хв = - ![]() = 1, ув = 1 - 2 · 1 + 4 = 3. Графік функції схематично зображено на малюнку . Функція спадає на проміжку (-∞; 1] і зростає на проміжку [1; +∞).
= 1, ув = 1 - 2 · 1 + 4 = 3. Графік функції схематично зображено на малюнку . Функція спадає на проміжку (-∞; 1] і зростає на проміжку [1; +∞).
Відповідь. 1) Спадає на (-∞; +∞); 2) спадає на (-∞; 1], зростає на [1; +∞).
2. Властивості основних видів функцій
Нагадаємо, як за допомогою геометричних перетворень графіків функцій можна будувати графіки інших функцій.
Побудова графіка функції у = f(x) ± n, де n > 0
Щоб побудувати графік функції у = f(x) + n, де n > 0, достатньо графік функції у = f(x) перенести вздовж осі у на n одиниць вгору.
Щоб побудувати графік функції у = f(x) - n, де n > 0, достатньо графік функції у = f(x) перенести вздовж осі у на n одиниць униз
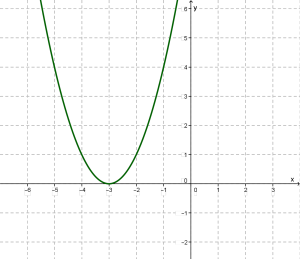
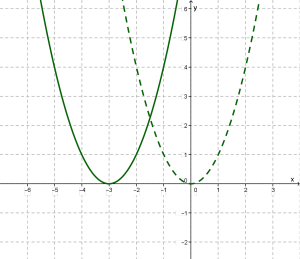
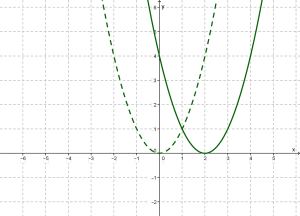
Приклад 2. Побудувати графіки функцій у = ![]() + 2 і у =
+ 2 і у = ![]() - 3.
- 3.
Розв’язання. Перетворимо графік функції у = ![]() . Графіки функцій у =
. Графіки функцій у = ![]() + 2 і у =
+ 2 і у = ![]() - 3 зображено на малюнку 4.11.
- 3 зображено на малюнку 4.11.

Мал. 7

Наприклад, графік функції
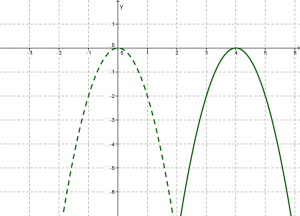
щоб побудувати графік функції
Тема уроку: Тригонометричні функції.
Презентація Властивості та графіки тригонометричних функцій.
Відеоуроки
Тема уроку: Основні співвідношення між тригонометричними функціями одного аргументу
https://naurok.com.ua/prezentaciya-tema-osnovni-spivvidnoshennya-mizh-trigonometrichnimi-funkciyami-odnogo-argumentu-230110.html
Презентація Тема.Основні співвідношення між тригонометричними функціями одного аргументу
Тема уроку: Визначений інтеграл його властивості фізичний та геометричний зміст.
Відеоуроки
Презентація Інтеграл та його застосування.
Тема уроку: Похідна. Її застосування
Геометрія
Тема уроку: Паралельність прямих і площин
Презентація Паралельність прямих та площин
Тема уроку: Перпендикулярність прямих і площин.
Де використовують поняття паралельності та перпендикулярності в житті? Пропоную переглянути добірку.
Паралельні і перпендикулярні прямі в нашому житті.
Відеоуроки














Немає коментарів:
Дописати коментар